התפלגות נורמלית

Normal distribution

ההתפלגות הנורמלית היא מושג מפתח בהסתברות ובסטטיסטיקה.

מאפיינים

ההתפלגות הנורמלית היא אחת מההתפלגויות הרציפות החשובות והשימושיות ביותר.  

התפלגויות אמפיריות של תופעות רבות במציאות הן בעלות התפלגות נורמלית בקירוב.

סימון:

X\sim\ N(\mu,\sigma^2)

הערכים האפשריים של משתנה מקרי נורמלי:   רצף המספרים ממינוס אינסוף ועד אינסוף.

שני הפרמטרים של ההתפלגות:  

\mu \ \ ,\ \sigma^2

האות היוונית מיו מייצגת את התוחלת (ציר הסימטריה)

E\left(X\right)=\mu

האות היוונית סיגמה בריבוע מייצגת את השונות (מידת הפיזור), והשורש של השונות, סיגמה, היא סטיית התקן

Var\left(X\right)=\sigma^2     \\ {} \\  \sqrt{Var\left(X\right)}=\sigma

פונקציית הצפיפות:

f\left(x\right)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{{(x-\mu)}^2}{2\sigma^2}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -\infty<x<\infty\ \ \ \ \ \ \ \ 

התפלגות נורמלית היא התפלגות פעמונית וסימטרית.

להלן שרטוט של שלוש התפלגויות נורמליות על אותו ציר של ערכי המשתנה :

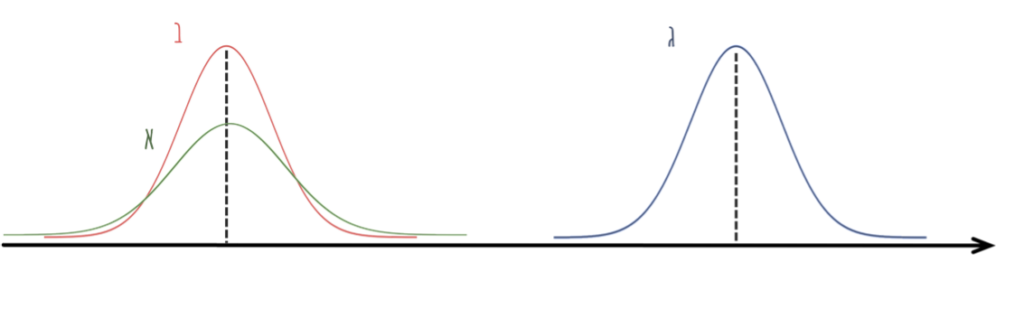
בהתפלגויות א׳ ו- ב׳ אותה תוחלת.

בהתפלגויות ב׳ ו- ג׳ אותה שונות.

שמות נוספים להתפלגות נורמלית: התפלגות גאוס/גאוסיאנית (על שם Carl Friedrich Gauss).

עקרונות בחישוב הסתברויות עם התפלגות נורמלית

• ההתפלגות הנורמלית סימטרית סביב התוחלת. 
• סך השטח מתחת לעקומת ההתפלגות שווה ל- 1.
• שטח = הסתברות.
• השטח מימין לערך מסוים שווה ל 1 פחות השטח משמאל לערך זה.
• חישוב שטח בין שני ערכים נעשה ע”י הפחתת שטחים: השטח משמאל לערך הגדול פחות השטח משמאל לערך הקטן.

כלל ה 68% – 95% – 99.7%  (החוק האמפירי)

כלל זה נקרא גם ״החוק האמפירי״ כיוון שהוא מתקיים בהתפלגויות אמפיריות רבות. 

כלומר:   

כ- 68%  מהנתונים נמצאים במרחק של עד סטיית תקן אחת מהממוצע.

כ- 95% מהנתונים נמצאים במרחק של עד 2 סטיות תקן מהממוצע. 

כמעט כל הנתונים נמצאים במרחק של עד 3 סטיות תקן מהממוצע.

ההתפלגות הנורמלית הסטנדרטית Standard normal distribution

סימון:

Z\sim\ N(0,1)

ההתפלגות הנורמלית הסטנדרטית היא התפלגות נורמלית מיוחדת, ובה התוחלת שווה ל 0 והשונות שווה ל 1.

נהוג לסמן את המשתנה הנורמלי הסטנדרטי ב Z . 

נהוג לסמן את פונקציית ההתפלגות המצטברת של מ״מ נורמלי סטנדרטי באות היוונית פי:

\Phi(z)

כלומר:

\Phi\left(z\right)=P(Z\le z)

השטח מתחת לפונקציית הצפיפות הנורמלית הסטנדרטית, משמאל לערך z. 

שימו לב: התפלגות נורמלית סטנדרטית היא התפלגות סימטרית סביב 0 .

טבלת Z

להלן דוגמה לטבלה עבור ההתפלגות הנורמלית הסטנדרטית. בטבלה ישנם ערכים של המשתנה הנורמלי הסטנדרטי ושטחים (=הסתברויות). לכל ערך מופיע השטח משמאלו, כלומר:

\Phi\left(z\right)=P(Z\le z)

בשולי הטבלה (בצהוב) מופיעים ערכי Z. 

בעמודה השמאלית: ספרת האחדות וכן הספרה הראשונה אחרי הנקודה העשרונית, ובשורה העליונה: הספרה השנייה אחרי הנקודה העשרונית. 

בתוך הטבלה (בתכלת) מופיעים שטחים משמאל לערך הנתון של Z.

כללי עבודה עם התפלגות נורמלית סטנדרטית

חישוב שטח (הסתברות) משמאל לערך חיובי של Z :

זהו החישוב הפשוט ביותר, כיוון שבטבלה יש שטחים משמאל עבור ערכי  Z אי-שליליים.

חישוב שטח מימין לערך חיובי של Z :

נעזרים בעובדה כי סך השטח מתחת להתפלגות שווה ל- 1:

P\left(Z>z\right)=1-P\left(Z\le z\right)=1-\Phi\left(z\right)

חישוב שטח משמאל לערך שלילי של Z :

נעזרים בסימטריה של ההתפלגות הנורמלית הסטנדרטית סביב 0 :

\Phi\left(-z\right)=1-\Phi\left(z\right)

חישוב שטח מימין לערך שלילי של Z :

נעזרים בסימטריה של ההתפלגות הנורמלית הסטנדרטית סביב 0 :

P\left(Z>-z\right)=1-\Phi\left(-z\right)=\Phi\left(z\right)

חישוב שטח בין שני ערכים:

P\left(a\le Z\le b\right)=\Phi\left(b\right)-\Phi\left(a\right)

מציאת ערך של Z שהשטח משמאלו נתון.

השטח משמאל ניתן לביטוי כהסתברות או כאחוזים. הערך המבוקש מכונה אחוזון (percentile). 

למשל: הערך z, שהשטח משמאלו הוא 0.9 (90%) נקרא ״אחוזון 90״ (עשירון עליון) וערכו 1.28.

תהליך החישוב ״הפוך״ : מוצאים שטח בתוך הטבלה, ויוצאים לשוליים כדי לקבל את הערך של Z .

הסימון לערך בהתפלגות הנורמלית הסטנדרטית שהשטח משמאלו הוא p :

z_p

למשל, אחוזון 90 מסומן:

z_{0.9}=1.28

קשר חשוב:

z_p=-z_{1-p}

 קשר זה נובע ממתכונת הסימטריה של ההתפלגות הנורמלית הסטנדרטית סביב 0 . 

תקנון Standardization 

על-מנת לחשב הסתברויות בהתפלגות נורמלית כלשהי, שאינה סטנדרטית, יש לבצע תקנון (סטנדרטיזציה).

נוסחת התקנון

עבור משתנה מקרי X עם תוחלת 

E\left(X\right)=\mu

 ושונות

Var\left(X\right)=\sigma^2

נגדיר משתנה מקרי חדש באופן הבא: 

Z=\frac{X-\mu}{\sigma}

למשתנה המקרי  Z  יש תוחלת 0 ושונות 1 .

Z הוא משתנה מקרי מתוקנן.

שימו לב: המונה מבטא הזזה של ההתפלגות,  וכתוצאה מכך התוחלת תהיה 0. החלוקה בסטיית התקן של X מבטלת את יחידות המדידה של X  ומשנה את הפיזור. כתוצאה מכך השונות תהיה 1. לכן המשתנה נקרא ״מתוקנן״. יוצרים התפלגות חדשה שבה התוחלת היא 0 והשונות 1. 

לכל ערך a של X, הערך המתוקנן של a מחושב לפי נוסחת התקנון, כלומר:

\frac{a-\mu}{\sigma}

הערך הזה נקרא גם ציון תקן, ערך תקן (standard score).

המשמעות של הערך המתוקנן:

הערך המתוקנן של a  מבטא את המרחק של הערך a  מהתוחלת, ביחידות של סטיית תקן . ערך מתוקנן חיובי: הערך גדול מהתוחלת. ערך מתוקנן שלילי: הערך קטן מהתוחלת. ערך מתוקנן 0 : הערך שווה לתוחלת.

תקנון של משתנה מקרי נורמלי

בהתפלגות נורמלית, התקנון מעביר להתפלגות נורמלית סטנדרטית.

כלומר:   עבור

X\sim\  N(\mu\ ,\ \sigma^2)

 המשתנה המקרי המתוקנן הוא:  

Z=\frac{X-\mu}{\sigma}

ומתקיים:

Z\sim\  N(0\ ,\ 1)

כללים לחישוב הסתברויות בהתפלגות נורמלית לא סטנדרטית 

X\sim\  N(\mu\ ,\sigma^2)

חישוב שטח (הסתברות) משמאל לערך נתון של  X : מחשבים את ציון התקן, ומוצאים את השטח המתאים בטבלה של ההתפלגות הנורמלית הסטנדרטית.

P\left(X\le a\right)=\Phi\left(\frac{a-\mu}{\sigma}\right)

חישוב שטח מימין לערך נתון של X : 

P\left(X>a\right)=1-\Phi\left(\frac{a-\mu}{\sigma}\right)

חישוב שטח בין שני ערכים של X :

P\left(a\le X\le b\right)=\Phi\left(\frac{b-\mu}{\sigma}\right)-\Phi\left(\frac{a-\mu}{\sigma}\right)

מציאת הערך של X שהשטח משמאלו נתון (חישוב ״הפוך״):

• מוצאים את השטח בטבלת ההתפלגות הנורמלית הסטנדרטית.
• מוצאים את הערך של Z (בשולי הטבלה).
• מחשבים את הערך של X לפי הנוסחה: 

X=Z\cdot\sigma+\mu

ההתפלגות הנורמלית משמשת כקירוב להרבה התפלגות תיאורטיות ואמפיריות, בפרט בקירוב נורמלי להתפלגות בינומית ומשפט הגבול המרכזי.

אז בין אם אתם רוצים ללמוד על ההתפלגות הנורמלית, ובין אם אתם רוצים להעמיק את ההבנה שלכם בנושאים נוספים בהסתברות, הקורס שלנו כולל את כל מה שאתם צריכים כבסיס להצלחתכם.

הירשמו עכשיו וגלו את העוצמה של למידה מבוססת אנימציה!ואגב, אם תזדקקו לעזרה, תוכלו תמיד לפנות אלינו